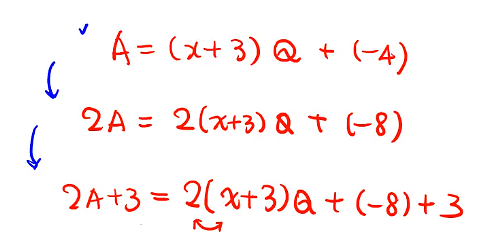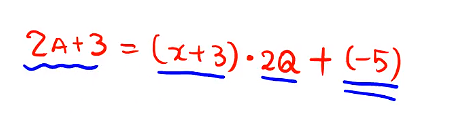怎麼求餘式？直接除嗎？
(2A+3) 直接除以 x+3 算得出來嗎？
因為題目沒有給 A，看起來似乎行不通！
看到「餘式」，同學還會想到什麼？
當然就是除法原理呀 ~ 被除式 ＋除式 x 商式 + 餘式
接著唯一能做的，好像只能觀察這個式子，
看看能不能殺出一條解路。
-
00:00
1.
重要題型 6
播放影片: https://k12.xms.tw/media/98
解題分析
- 1.
- 2.將題目的條件，改成「除法原理」的形式既然要朝「除法原理」試試看，接下來，當然就把題目的條件，先整理成除法原理的形式，再做下一步的觀察啦。
- 3.為什麼從 A 換成 2A+3？因為兩式的除式相同 (x+3)所以藉由已知去找 (2A+3) 除以 (x+3) 的餘式怎麼做呢?很簡單！等量公理就搞定！整理後，答案幾乎就可以對照出來了！
- 4.求餘式？很直覺，只要看餘式的部分就好！因為這就是餘式的定義 (除法原理)。其他的 (包括 Q)，一點都不重要了。
評語
請登入後才可以評分
- 位置
-
- 資料夾名稱
- [週刊] 乘法公式與多項式 (1~3 週)
- 發表人
- 林俊志
- 單位
- 台灣數位學苑 (k12 數學)
- 建立
- 2017-10-20 15:53:00
- 最近修訂
- 2021-05-27 16:45:26
- 長度
- 03:14
- 引用
- 1