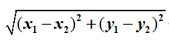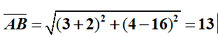平面上兩點 A(x1, x2), B(x2, y2) 的距離，關鍵是什麼？
只有一個，
就是「x, y 座標相減的平方和開根號」
也就是 
例如： A( 3, 4) B(-2, 16)
則 
-
00:00
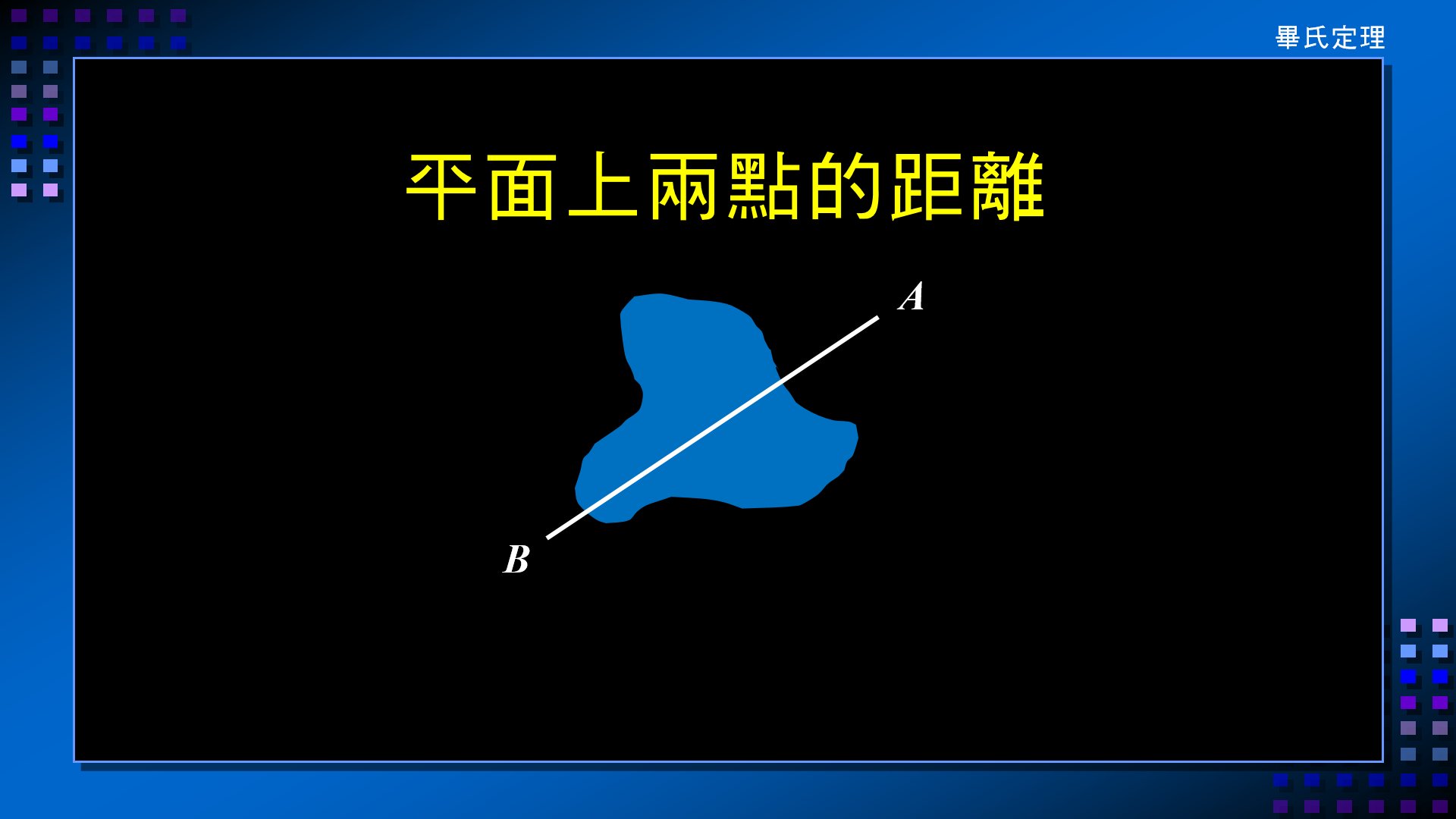
1.
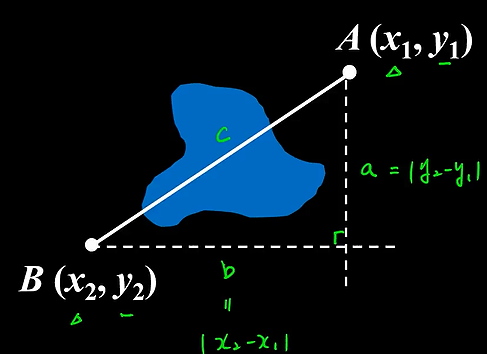
平面上兩點的距離
-
01:22
2.
數線上兩點的距離
-
02:20
3.
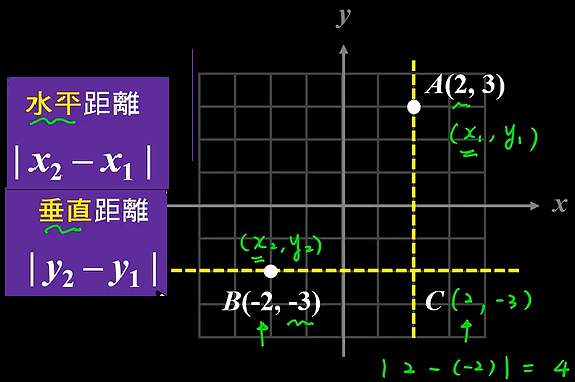
兩點間的水平距離
-
03:53
4.
平面上兩點的距離公式
-
05:44
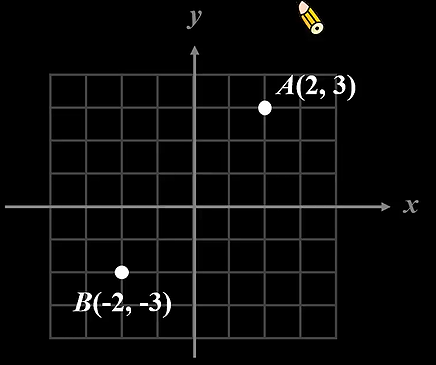
5.
例題練習
-
00:00
1.
平面上兩點的距離
-
01:22
2.
數線上兩點的距離
-
02:20
3.
兩點間的水平距離
-
03:53
4.
平面上兩點的距離公式
-
05:44
5.
例題練習
- 位置
-
- 資料夾名稱
- 平方根與畢氏定理 (ch2)
- 發表人
- 顧震宇
- 單位
- 台灣數位學苑 (k12 數學)
- 建立
- 2018-07-01 01:25:31
- 最近修訂
- 2021-07-24 00:39:52
- 長度
- 07:01
- 引用
- 1