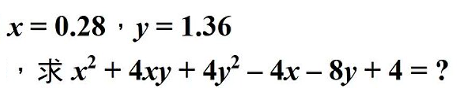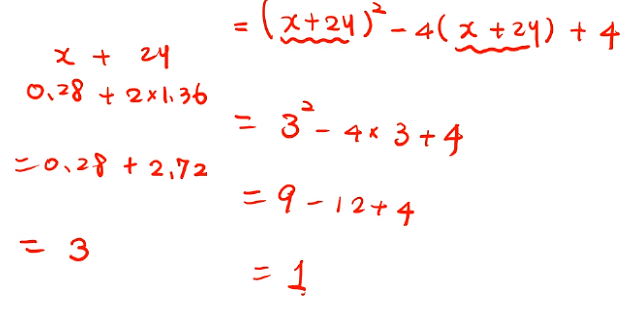-
00:00
1.
和的平方公式
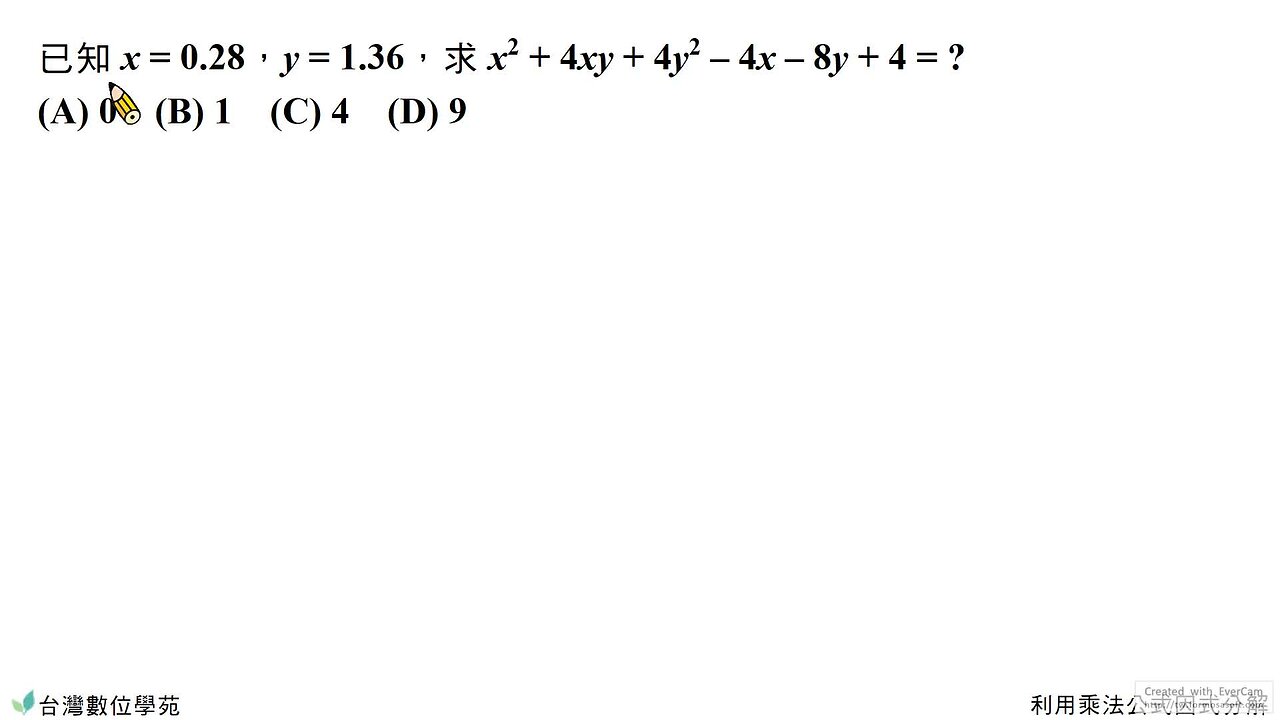
播放影片: https://k12.xms.tw/media/3116
重點
- 1.
- 動動腦時間~當算出 (x + 2y)2 ─ 4(x + 2y) + 4 時,能不能再繼續化簡呢? 該怎麼做呢?........注意到 4 = 22 ,如果把 (x + 2y)2 當作 a ,一樣可以利用 a2 ─ 4a + 4 (差的平方公式) 化簡得到 (x + 2y ─ 2)2,計算上會更快一點呢!
評語
請登入後才可以評分
- 位置
-
- 資料夾名稱
- 因式分解 (ch3)
- 上傳者
- 高帆萱
- 單位
- 台灣數位學苑 (k12 數學)
- 建立
- 2021-07-28 17:42:40
- 最近修訂
- 2021-12-14 13:20:09
- 長度
- 02:10
- 引用
- 1