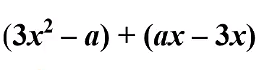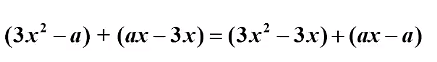講者：蘇德宙
日期：2018-07-01
觀看: 1543
  • 00:00 1.
    因式分解 ~ 分組提公因式
  • 01:17 2.
    要怎麼分組？
  • 02:39 3.
    觀念練習
  • 03:54 4.
    例題練習 ~ 重新分組
  • 05:06 5.
    重點整理
  • 索引
  • 筆記
  • 討論
  • 全螢幕
因式分解 (分組分解)
長度: 06:01, 瀏覽: 1544, 最近修訂: 2021-07-28 我要推薦
重點
  1. 1.
    為什麼要分組再提公因式？
    因為不是所有項都有相同的公因式
     
    例如： 2x2 + 3x ─ 2x ─ 3，沒有四項都有的公因式，
    但是！若先將第 1、3 項、第 2、4 項分組，
    (2x2 ─ 2x) +(3x ─ 3) = 2x(x ─ 2) +3(x ─ 2)
                                     = (2x + 3)(x ─ 2)
    就出現公因式可以提出，就可以完成因式分解了！
     
  2. 2.
    分組提公因式，關鍵是「觀察」！
    非常重要，不是隨便亂分喔！
    先仔細觀察係數及符號，
    分組後才有辦法提公因式。
  3. 3.
    每題只有一種分組方法嗎？
    不是的，依照題目，也可能有其他的分組方式
     
    例如：上題中 2x2 + 3x ─ 2x ─ 3 
    把前兩個分成一組、後兩個一組，一樣可以求出答案，
     2x2 + 3x ─ 2x ─ 3 = x(2x + 3) ─ (2x + 3)
                                  = (x ─ 2) (x + 3)
     
    分組的方法不是唯一，也不是只有一種作法，
    同學掌握「先觀察公因式再分組」的原則，
    大多數的題目都可以迎刃而解，
     
  4. 4.
    題目已經分好組卻沒有公因式，怎麼辦？
    通常題目都是故意的，
    同學不妨將括號打開，重新觀察式子再分組，
    才有辦法完成因式分解。
     
    評語
    請登入後才可以評分
    上一篇 下一篇
    • 00:00 1.
      因式分解 ~ 分組提公因式
    • 01:17 2.
      要怎麼分組？
    • 02:39 3.
      觀念練習
    • 03:54 4.
      例題練習 ~ 重新分組
    • 05:06 5.
      重點整理
    位置
    1. 知識庫
    2. ...
    3. 因式分解 (ch3)
    資料夾名稱
    因式分解 (ch3)
    發表人
    顧震宇
    單位
    台灣數位學苑 (k12 數學)
    建立
    2018-07-01 01:36:53
    最近修訂
    2021-07-28 16:01:22
    長度
    06:01
    引用
    1
    1. 知識庫
    2. ...
    3. 因式分解 (ch3)
    1. 1.
      因式、倍式與因式分解 (觀念)
      1. 1.1
        因式、倍式
      2. 1.2
        因式分解
    2. 2.
      因式、倍式與因式分解 (例題)
      1. 2.1
        [例] 因式、倍式與因式分解
      2. 2.2
        [綜] 因式、倍式與因式分解 ~ 基礎
    3. 3.
      因式分解的方法 ~ 提出公因式 (觀念)
      1. 3.1
        因式分解 (提出公因式)
      2. 3.2
        因式分解 (分組分解)
    4. 4.
      因式分解的方法 ~ 提出公因式 (例題)
      1. 4.1
        [例] 提出公因式
      2. 4.2
        [例] 分組分解
      3. 4.3
        [綜] 提出公因式法 ~ 基礎
      4. 4.4
        [綜] 提出公因式法 ~ 考題 1
      5. 4.5
        [綜] 提出公因式法 ~ 考題 2
    5. 5.
      因式分解的方法 ~ 利用乘法公式 (觀念)
      1. 5.1
        因式分解 (和、差的平方公式)
      2. 5.2
        因式分解 (平方差公式)
    6. 6.
      因式分解的方法 ~ 利用乘法公式 (例題)
      1. 6.1
        [例] 完全平方公式
      2. 6.2
        [例] 平方差公式
      3. 6.3
        [例] 乘法公式綜合
      4. 6.4
        [綜] 利用乘法公式因式分解 ~ 基礎
      5. 6.5
        [綜] 利用乘法公式因式分解 ~ 考題 1
      6. 6.6
        [綜] 利用乘法公式因式分解 ~ 考題 2
    7. 7.
      因式分解的方法 ~ 十字交乘法 (觀念)
      1. 7.1
        十字交乘法
    8. 8.
      因式分解的方法 ~ 十字交乘法 (例題)
      1. 8.1
        [例] 十字交乘法_1
      2. 8.2
        [例] 十字交乘法_2
      3. 8.3
        [例] 十字交乘法_3
      4. 8.4
        [綜] 十字交乘法 ~ 基礎
      5. 8.5
        [綜] 十字交乘法 ~ 考題
    9. 9.
      因式題型3
    10. 10.
      因式題型2
    11. 11.
      因式題型1
    12. 12.
      因式、倍式 難題2
    13. 13.
      因式、倍式 難題1
    14. 14.
      難題 提公因式
    15. 15.
      難題 十字交乘1
    16. 16.
      難題 十字交乘法_2
    17. 17.
      難題 平方差公式
    18. 18.
      難題 乘法公式因式分解
    19. 19.
      難題 分組提公因式
    © Copyright since 2017 by FormosaSoft Corporation.
    All rights reserved.