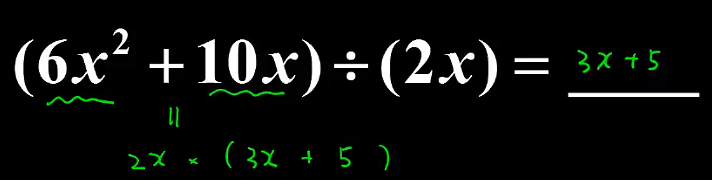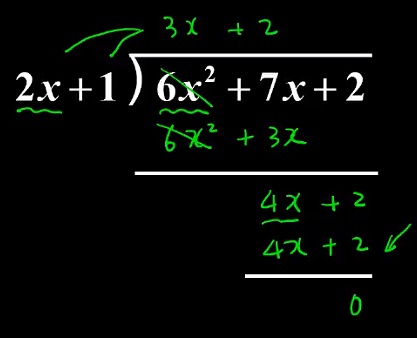怎麼做多項式的除法？
同學只要記得
除法其實就是乘法的反運算
例如：
24 ÷ 6 = 4
代表 4 x 6 =24
那麼多項式也是同樣的概念，
例如：(8x2) ÷ (2x)
等同於 ( 2x ) 乘以什麼會等於 8x2
那就是 4x 囉！
-
00:00
1.
多項式的除法
-
00:25
2.
單項式除法
-
01:35
3.
多項式 除以 單項式
-
02:30
4.
多項式的直式除法
-
04:58
5.
有缺項的直式除法
-
06:13
6.
餘式
-
07:26
7.
除法原理
-
08:39
8.
重點整理
播放影片: https://k12.xms.tw/media/692
重點
- 1.
- 2.除法中的餘式，最高次數不能大於除式？就像數字的除法中，餘數不能大於除數，同樣的，多項式的除法中，餘式的次數必須小於除式的次數，才算完成除法的計算例如：(6x2+7x+5) ÷ (2x+1) = 3x ...... (4x+5)顯然是不對的，因為 (4x+5) 可以繼續除，寫成 (6x2+7x+5) ÷ (2x+1) = (3x+2) ...... 3 才是正確的寫法
- 3.用直式做多項式除法，要特別注意什麼？有兩個規則需要同學特別注意
- 降冪排列 (從最高次開始做)
- 遇到缺項要補 0 (同類項才能合併)
這樣才能確保直式的除法不會計算錯誤
- 4.除法原理是什麼?其實很直覺，同學早就會了，只是把除法的四個要素，用乘法的概念寫下來而已。也就是「被除式 = 除式 x 商式 +餘式」例如：(2x2 + 3x -1) ÷ ( x+1) = (2x+1) ..... -2可以寫成(2x2 + 3x -1) = ( x+1)(2x+1) -2
- 5.怎麼利用「除法原理」解題？因為是等式，所以可以利用「等量公理」來運算例如，想要求 2(2x2 + 3x -1) 除以 (x+1) 的餘式已知 (2x2 + 3x -1) = (x+1)(2x+1) -2把兩邊同乘以 2，也就是2(2x2 + 3x -1) = 2(x+1)(2x+1) -4則根據除法原理，餘式就是 -4 ，是不是很簡單呢?當同學看到題目中有除法的要素時，馬上就要想到可以用除法原理表示喔！
評語
請登入後才可以評分
-
00:00
1.
多項式的除法
-
00:25
2.
單項式除法
-
01:35
3.
多項式 除以 單項式
-
02:30
4.
多項式的直式除法
-
04:58
5.
有缺項的直式除法
-
06:13
6.
餘式
-
07:26
7.
除法原理
-
08:39
8.
重點整理
- 位置
-
- 資料夾名稱
- 乘法公式與多項式 (ch1)
- 發表人
- 顧震宇
- 單位
- 台灣數位學苑 (k12 數學)
- 建立
- 2018-07-01 01:18:43
- 最近修訂
- 2021-07-28 05:44:12
- 長度
- 09:12
- 引用
- 1