-
00:00
1.
兩個直角的四邊形對角線
-
04:32
2.
圓內接四邊形對角互補
-
07:08
3.
斜邊中點是外心
-
09:58
4.
30 - 60 - 90 邊長比例
-
11:42
5.
證明
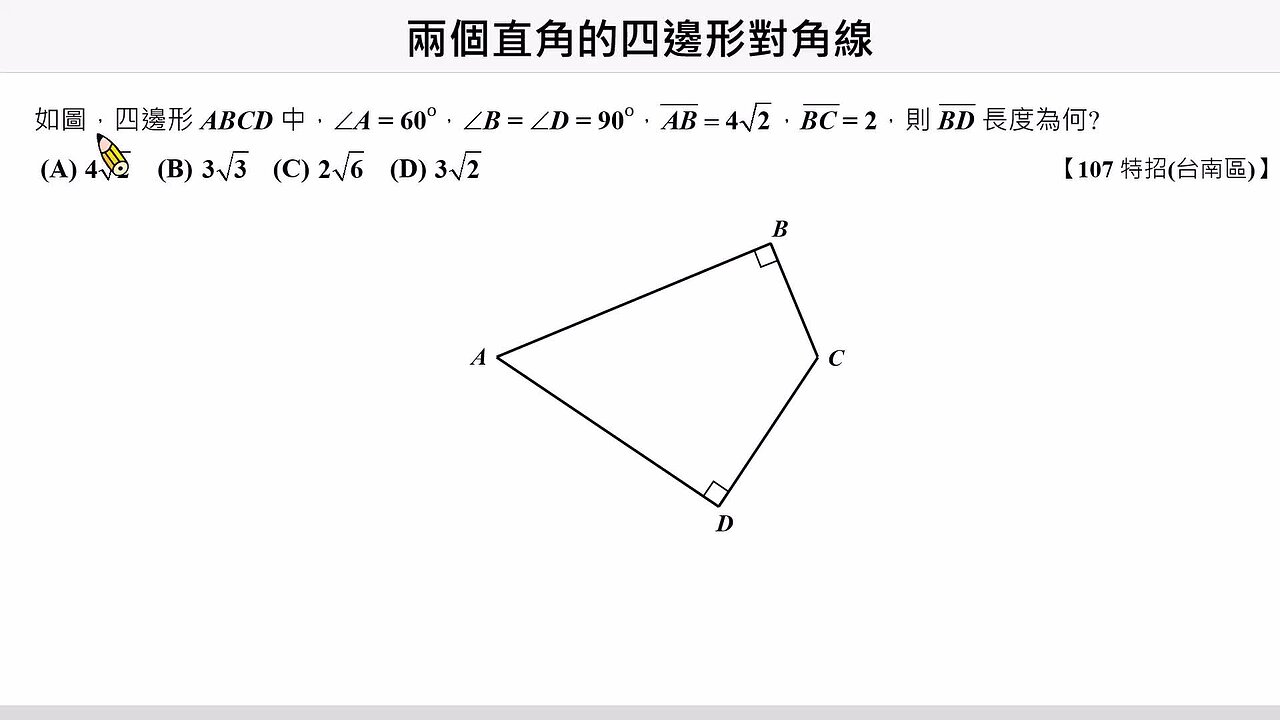
播放影片: https://k12.xms.tw/media/4184
解題的關鍵線索與性質:
- 看到對角互補,想到圓內接四邊形,畫輔助圓BD 為圓中的弦,欲求弦長,想到弦心距,需要先找圓心
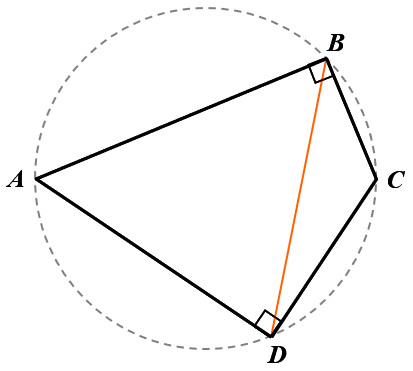
- 圓心為直角三角形斜邊 AC 中點(外心)

連出半徑及弦心距,思考畢氏定理 - 圓心角 = 弧 BD = 圓周角 A 的 2 倍 = 120 度
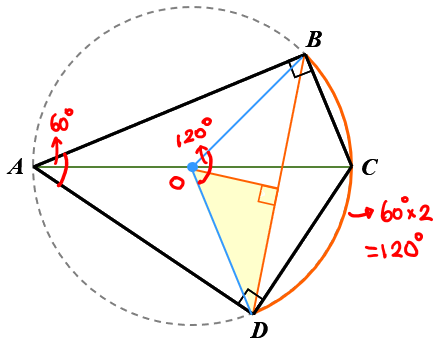
- OB = OD,角 D = 30 度,想起特殊角直角三角形邊長比

附件:
評語
請登入後才可以評分
-
00:00
1.
兩個直角的四邊形對角線
-
04:32
2.
圓內接四邊形對角互補
-
07:08
3.
斜邊中點是外心
-
09:58
4.
30 - 60 - 90 邊長比例
-
11:42
5.
證明
- 位置
-
- 資料夾名稱
- 每天 10 分鐘,會考 A++
- 上傳者
- 顧震宇
- 單位
- 台灣數位學苑 (k12 數學)
- 標籤
- 特殊直角三角形30-60-90, 圓心角, 弦, 弦心距, 圓周角, 圓內接四邊形, 對角互補
- 建立
- 2024-04-09 11:18:49
- 最近修訂
- 2025-06-09 21:37:34
- 長度
- 12:51