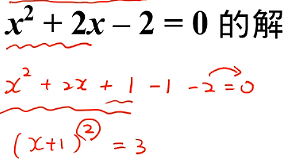講者：蘇德宙
日期：2018-07-01
觀看: 5968
  • 00:00 1.
    配方法
  • 02:13 2.
    觀念練習
  • 03:56 3.
    例題練習 ~ 湊成 2ab 的形式
  • 05:58 4.
    例題練習 ~ 平方項係數不是 1
  • 07:01 5.
    例題練習 ~ 常數項很大
  • 08:32 6.
    重點整理
  • 索引
  • 筆記
  • 討論
  • 全螢幕
配方法
長度: 10:24, 瀏覽: 5969, 最近修訂: 2021-07-30 我要推薦
重點
  1. 1.
    什麼是「配方法」？
    顧名思義，
    把式子配成「完全平方式」的方法。
    也就是寫成 (ax + b)2 = c 的形式。
     
     
  2. 2.
    配成「完全平方式」，要注意什麼
    要化簡成 (ax+b)2 = c ，
    二次項 (x2) 和一次項 (x) 要用「和 (差) 的平方公式」
    寫成「完全平方式」。
  3. 3.
    為什麼要學「配方法」？
    動機很單純，
    因為「平方根」解方程式很快很方便！
    例如： (x+1)2 = 9 ，很容易看出
     x = 3 ─ 1  = 2 以及 x = (─3) ─ 1  = ─ 4
     
    所以如果有方法可以把任意方程式，
    都寫成 (ax + b)2 = c 的形式，
    那就太好了！
     
    評語
    請登入後才可以評分
    上一篇 下一篇
    • 00:00 1.
      配方法
    • 02:13 2.
      觀念練習
    • 03:56 3.
      例題練習 ~ 湊成 2ab 的形式
    • 05:58 4.
      例題練習 ~ 平方項係數不是 1
    • 07:01 5.
      例題練習 ~ 常數項很大
    • 08:32 6.
      重點整理
    位置
    1. 知識庫
    2. ...
    3. 一元二次方程式 (ch4)
    資料夾名稱
    一元二次方程式 (ch4)
    發表人
    顧震宇
    單位
    台灣數位學苑 (k12 數學)
    建立
    2018-07-01 01:42:46
    最近修訂
    2021-07-30 16:46:59
    長度
    10:24
    引用
    1
    1. 知識庫
    2. ...
    3. 一元二次方程式 (ch4)
    1. 1.
      因式分解解一元二次方程式 (觀念)
      1. 1.1
        一元二次方程式
      2. 1.2
        解一元二次方程式
    2. 2.
      因式分解解一元二次方程式 (例題)
      1. 2.1
        [例] 一元二次方程式
      2. 2.2
        [例] 解一元二次方程式_1
      3. 2.3
        [例] 解一元二次方程式_2
      4. 2.4
        [綜] 一元二次方程式 ~ 基礎
      5. 2.5
        [綜] 一元二次方程式 ~ 考題
    3. 3.
      配方法與公式解 (觀念)
      1. 3.1
        利用平方根求方程式的解
      2. 3.2
        配方法
      3. 3.3
        公式解
      4. 3.4
        公式解 _ 判別式
    4. 4.
      配方法與公式解 (例題)
      1. 4.1
        [例] 配方法
      2. 4.2
        [例] 公式解
      3. 4.3
        [例] 判別式
      4. 4.4
        [綜] 配方法與公式解 ~ 基礎
      5. 4.5
        [綜] 配方法與公式解 ~ 考題
    5. 5.
      應用問題 (例題)
      1. 5.1
        [例] 應用問題
      2. 5.2
        [綜] 一元二次方程式應用問題 ~ 基礎
      3. 5.3
        [綜] 一元二次方程式應用問題 ~ 考題
    6. 6.
      [練習] 平方根解方程
    7. 7.
      [練習] [難題] 看錯問題
    8. 8.
      [練習] 方程式
    9. 9.
      [練習] 因式分解解方程式
    10. 10.
      [練習] 判別式
    11. 11.
      [難題] 方程式的解應用
    12. 12.
      [難題]根與係數應用
    13. 13.
      [難題]解方程式
    14. 14.
      [練習] 方程式的解還原
    15. 15.
      [練習] 配方法
    16. 16.
      [練習] 面積問題
    17. 17.
      [難題] 繩長問題
    18. 18.
      [練習] 數字問題
    19. 19.
      [練習] 分裝問題
    20. 20.
      [練習] 長度問題
    21. 21.
      配方法與公式解 _難題2
    22. 22.
      配方法與公式解 _ 難題1
    23. 23.
      一元二次方程式 _ 2難題
    24. 24.
      一元二次方程式 _ 難題1
    25. 25.
      一元二次方程式應用問題 難題
    26. 26.
      4-1 重點整理 (舊)
    27. 27.
      4-2 重點整理 (舊)
    28. 28.
      4-3 重點整理 (舊)
    29. 29.
      4-1 重點整理
    30. 30.
      4-2 重點整理
    31. 31.
      4-3 重點整理
    © Copyright since 2017 by FormosaSoft Corporation.
    All rights reserved.