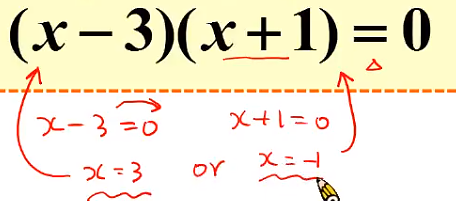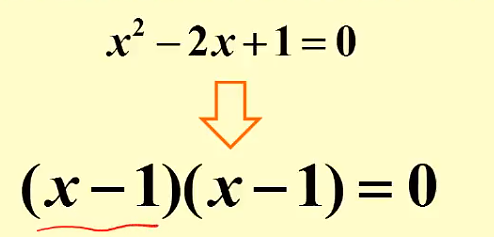講者：蘇德宙
日期：2018-07-01
觀看: 1175
  • 00:00 1.
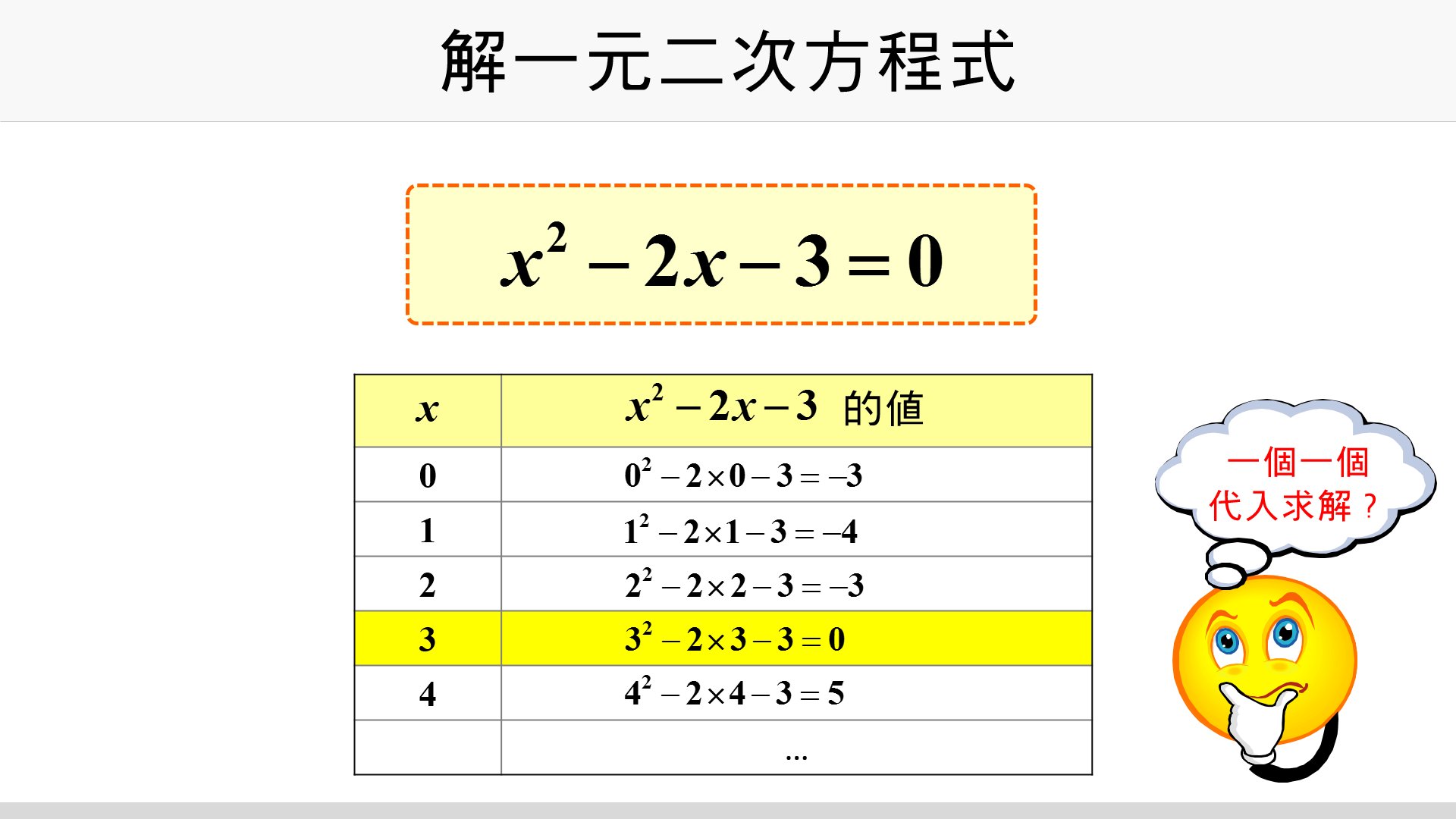
    解一元二次方程式
  • 01:01 2.
    利用因式分解求方程式的解
  • 02:44 3.
    觀念練習
  • 03:31 4.
    重根
  • 04:10 5.
    例題練習
  • 05:29 6.
    重點整理
  • 索引
  • 筆記
  • 討論
  • 全螢幕
解一元二次方程式
長度: 05:57, 瀏覽: 1176, 最近修訂: 2021-07-30 我要推薦
重點
  1. 1.
    可以用「代數字」的方式解方程式嗎？
    當然可以，
    但是每一題都必須要花很多時間嘗試，
    非常浪費時間。
     
    有沒有更快的方法解一元二次方程式呢？
  2. 2.
    因式分解解方程式，關鍵是什麼？
    同學要熟練上一章因式分解的技巧，才能加快解題的速度，
    其中會用到的技巧有：
    • 和、差的平方公式 
              例： 4x2 + 12x + 9 = 0 → (2x + 3)2 = 0
    • 平方差公式
              例：16x2 ─ 25 = 0 → (4x ─ 5)(4x + 5) =0
    • 十字交乘法
              例：x2 + 5x + 6 = 0 → (x + 3)(x + 2) = 0
     
  3. 3.
    因式分解解一元二次方程式，原理是什麼？
    很簡單喔，就是根據
    「若 a x b = 0 ，則 a = 0 或 b = 0」的性質。
     
    例如：
    (x+2)(x+1) = 0，由性質可知 x + 2 = 0 或  x + 1 = 0
    所以 x = ─ 2 或 ─ 1
     
     
  4. 4.
    什麼是「重根」？
    顧名思義，就是「重複的根」。
    一元二次方程式的兩個根如果一樣，
     
    例如：
    (x ─ 1)2 = 0 兩根都是 1 ，就稱 1 方程式的重根
    評語
    請登入後才可以評分
    上一篇 下一篇
    • 00:00 1.
      解一元二次方程式
    • 01:01 2.
      利用因式分解求方程式的解
    • 02:44 3.
      觀念練習
    • 03:31 4.
      重根
    • 04:10 5.
      例題練習
    • 05:29 6.
      重點整理
    位置
    1. 知識庫
    2. ...
    3. 一元二次方程式 (ch4)
    資料夾名稱
    一元二次方程式 (ch4)
    發表人
    顧震宇
    單位
    台灣數位學苑 (k12 數學)
    建立
    2018-07-01 01:42:47
    最近修訂
    2021-07-30 15:44:20
    長度
    05:57
    引用
    1
    1. 知識庫
    2. ...
    3. 一元二次方程式 (ch4)
    1. 1.
      因式分解解一元二次方程式 (觀念)
      1. 1.1
        一元二次方程式
      2. 1.2
        解一元二次方程式
    2. 2.
      因式分解解一元二次方程式 (例題)
      1. 2.1
        [例] 一元二次方程式
      2. 2.2
        [例] 解一元二次方程式_1
      3. 2.3
        [例] 解一元二次方程式_2
      4. 2.4
        [綜] 一元二次方程式 ~ 基礎
      5. 2.5
        [綜] 一元二次方程式 ~ 考題
    3. 3.
      配方法與公式解 (觀念)
      1. 3.1
        利用平方根求方程式的解
      2. 3.2
        配方法
      3. 3.3
        公式解
      4. 3.4
        公式解 _ 判別式
    4. 4.
      配方法與公式解 (例題)
      1. 4.1
        [例] 配方法
      2. 4.2
        [例] 公式解
      3. 4.3
        [例] 判別式
      4. 4.4
        [綜] 配方法與公式解 ~ 基礎
      5. 4.5
        [綜] 配方法與公式解 ~ 考題
    5. 5.
      應用問題 (例題)
      1. 5.1
        [例] 應用問題
      2. 5.2
        [綜] 一元二次方程式應用問題 ~ 基礎
      3. 5.3
        [綜] 一元二次方程式應用問題 ~ 考題
    6. 6.
      [練習] 平方根解方程
    7. 7.
      [練習] [難題] 看錯問題
    8. 8.
      [練習] 方程式
    9. 9.
      [練習] 因式分解解方程式
    10. 10.
      [練習] 判別式
    11. 11.
      [難題] 方程式的解應用
    12. 12.
      [難題]根與係數應用
    13. 13.
      [難題]解方程式
    14. 14.
      [練習] 方程式的解還原
    15. 15.
      [練習] 配方法
    16. 16.
      [練習] 面積問題
    17. 17.
      [難題] 繩長問題
    18. 18.
      [練習] 數字問題
    19. 19.
      [練習] 分裝問題
    20. 20.
      [練習] 長度問題
    21. 21.
      配方法與公式解 _難題2
    22. 22.
      配方法與公式解 _ 難題1
    23. 23.
      一元二次方程式 _ 2難題
    24. 24.
      一元二次方程式 _ 難題1
    25. 25.
      一元二次方程式應用問題 難題
    26. 26.
      4-1 重點整理 (舊)
    27. 27.
      4-2 重點整理 (舊)
    28. 28.
      4-3 重點整理 (舊)
    29. 29.
      4-1 重點整理
    30. 30.
      4-2 重點整理
    31. 31.
      4-3 重點整理
    © Copyright since 2017 by FormosaSoft Corporation.
    All rights reserved.